Real vs Complex Plane | Gaurish4Math
Complex Numbers and the SHO
Harmonic function - Wikipedia
A particle moving in the complex plane can bypass the node at the... | Download Scientific Diagram
Complex plane & oscillator – TikZ.net
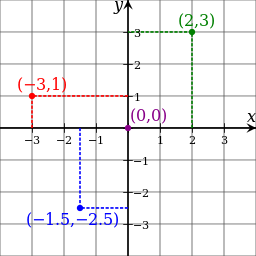
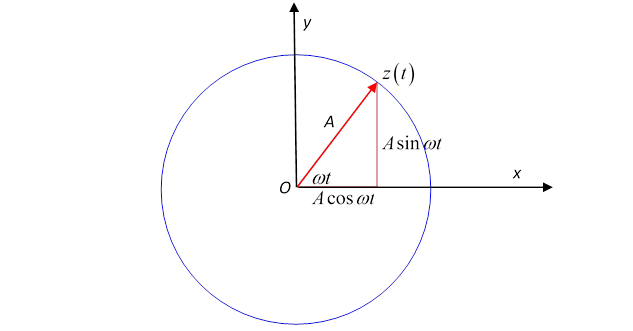
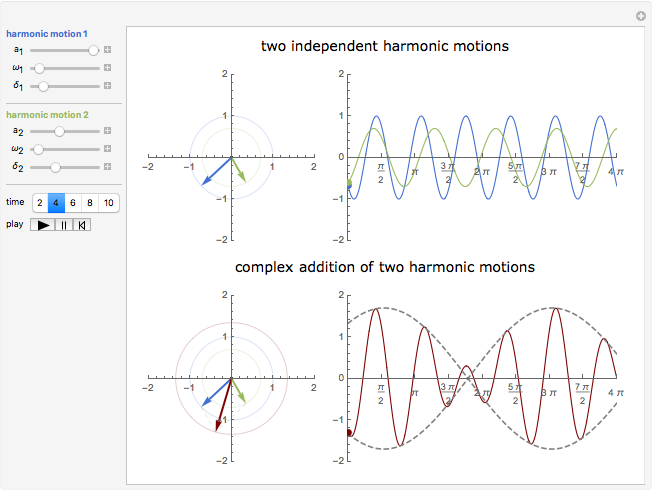
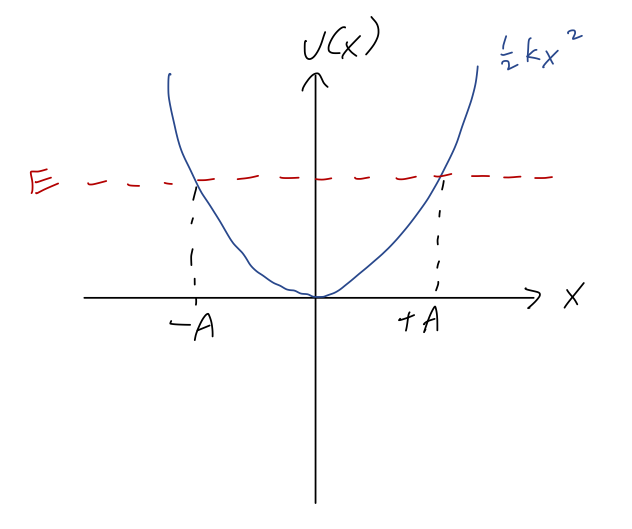
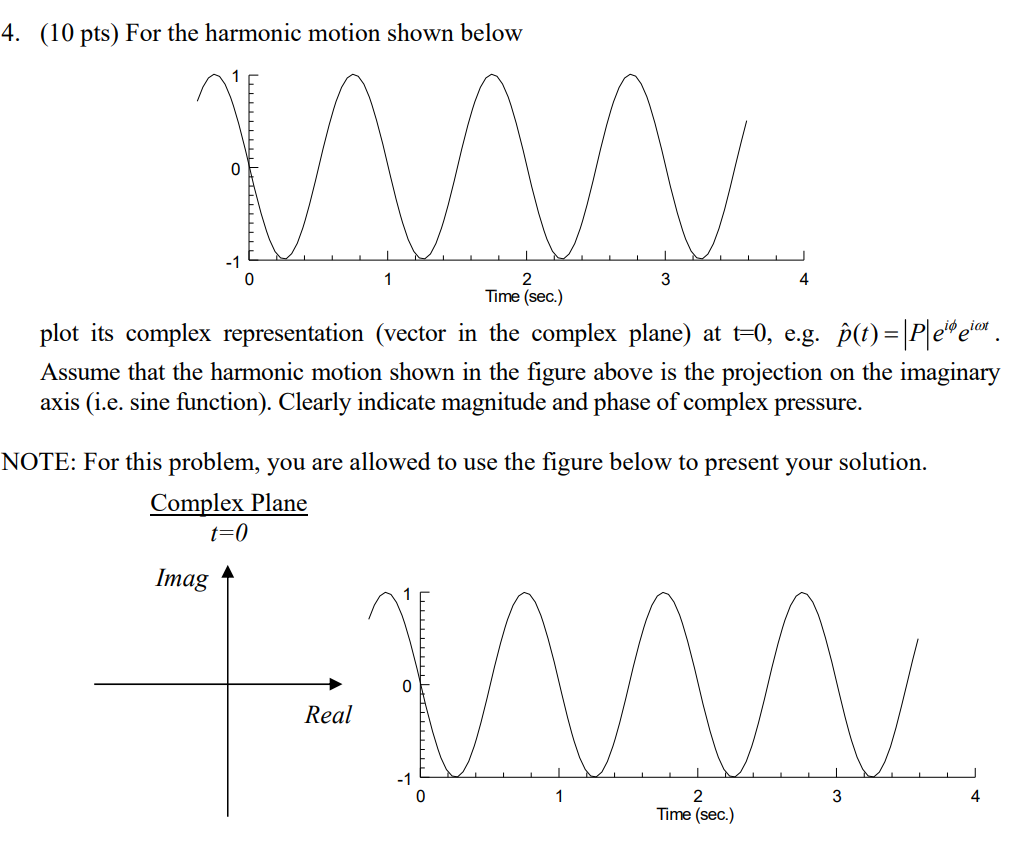
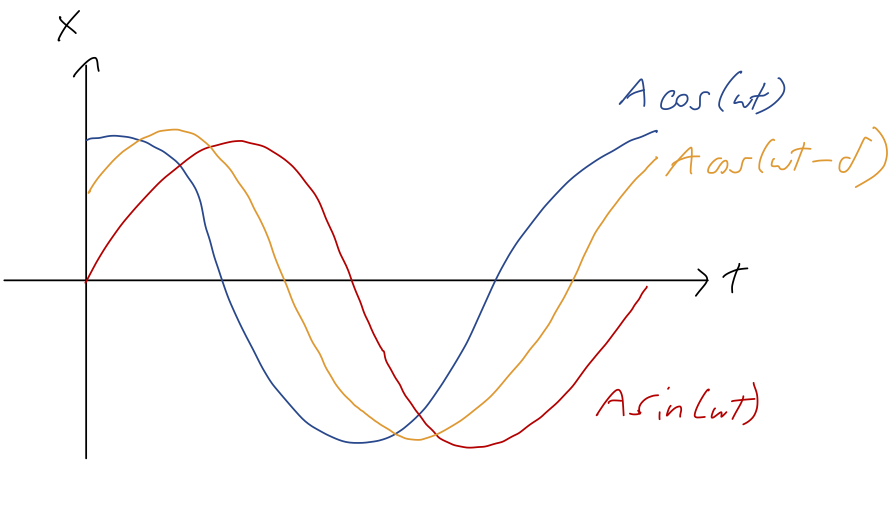
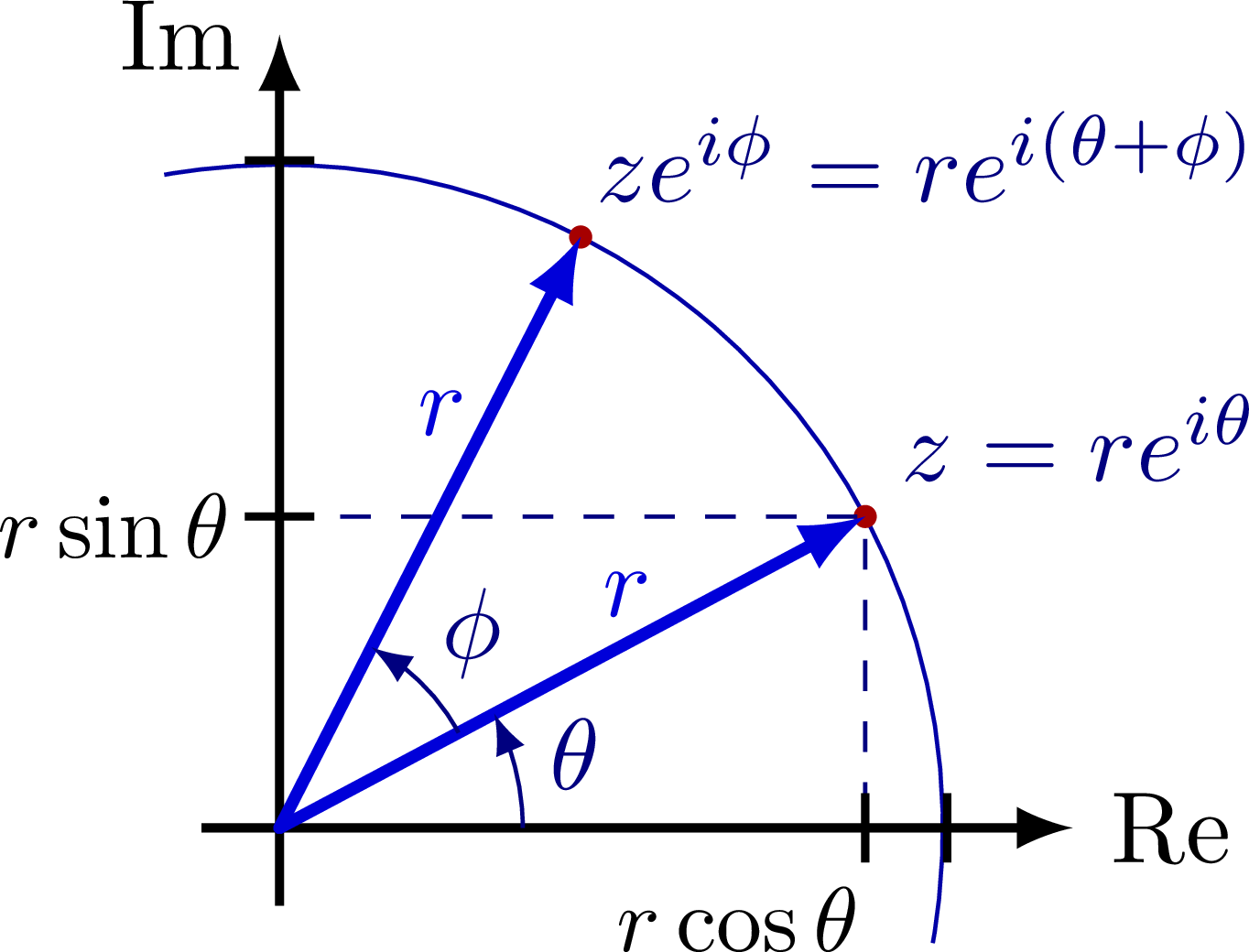Complex Representation of Harmonic Oscillations. The imaginary number i is defined by i 2 = -1. Any complex number can be written as z = x + i y where. - ppt download
Complex Spherical Harmonics - Wolfram Demonstrations Project
Complex plane: main torques and motions involved in the analysis. | Download Scientific Diagram
How do complex numbers actually apply to control systems? - YouTube
1: Harmonic variation of electric field E and current J with time t.... | Download Scientific Diagram
Complex Representation of Harmonic Oscillations. The imaginary number i is defined by i 2 = -1. Any complex number can be written as z = x + i y where. - ppt download
Complex Addition of Harmonic Motions and the Phenomenon of Beats - Wolfram Demonstrations Project
Why do we represent the imaginary part of an imaginary number with a sine wave? - Quora
Harmonic oscillators and complex numbers
Complex Numbers & Phasors in Polar and Rectangular Form
DFT calculated second harmonic generation. Real part, imaginary part,... | Download Scientific Diagram
Complex Representation of Harmonic Oscillations. The imaginary number i is defined by i 2 = -1. Any complex number can be written as z = x + i y where. - ppt download
Complex Numbers and the SHO
Complex Representation of Harmonic Oscillations. The imaginary number i is defined by i 2 = -1. Any complex number can be written as z = x + i y where. - ppt download
Harmonic oscillators and complex numbers
Complex Addition of Harmonic Motions and the Phenomenon of Beats - Wolfram Demonstrations Project
Solved 4. (10 pts) For the harmonic motion shown below -1 4 | Chegg.com
Complex Numbers and the SHO
Solved d is a region on the complex plane LetthatSignature. | Chegg.com
Complex plane - Wikipedia
