PPLATO | FLAP | PHYS 11.2: The quantum harmonic oscillator
Harmonic Oscillator
PPLATO | FLAP | PHYS 11.2: The quantum harmonic oscillator
Partition Function - an overview | ScienceDirect Topics
SOLVED: To relax the restriction that N = Ns we now analyze the system in the grand canonical ensemble where the lattice is in contact with a heat and par ticle reservoir
MIDTERM EXAM PHGN530 Statistical Mechanics Note: You can collaborate with anyone including your classmates. In fact, you should
Quantum harmonic oscillator - Wikiwand
8.044 Lecture Notes Chapter 6: Statistical Mechanics at Fixed Temperature (Canonical Ensemble)
2. Consider a system of n independent distinguishable | Chegg.com
PHYC - 505: Statistical Mechanics Midterm Exam 1 Solutions
Quantum harmonic oscillator - Wikipedia
Solved solve the case of a system of N distinguishable | Chegg.com
Harmonic Oscillator and Density of States — Statistical Physics Notes
Chapter 8 Microcanonical ensemble
Solved 6.I0 points) Classical simple harmonic oscillators 1 | Chegg.com
Quantum harmonic oscillator - Wikipedia
SOLVED: Consider a system of many identical harmonic oscillators. Each harmonic oscillator has its energy of , 2) ho with n-0, 1,2, 8. Assuming they are distinguishable; (a) find the partition function
Solved 3. Consider a system of N distinguishable classical | Chegg.com
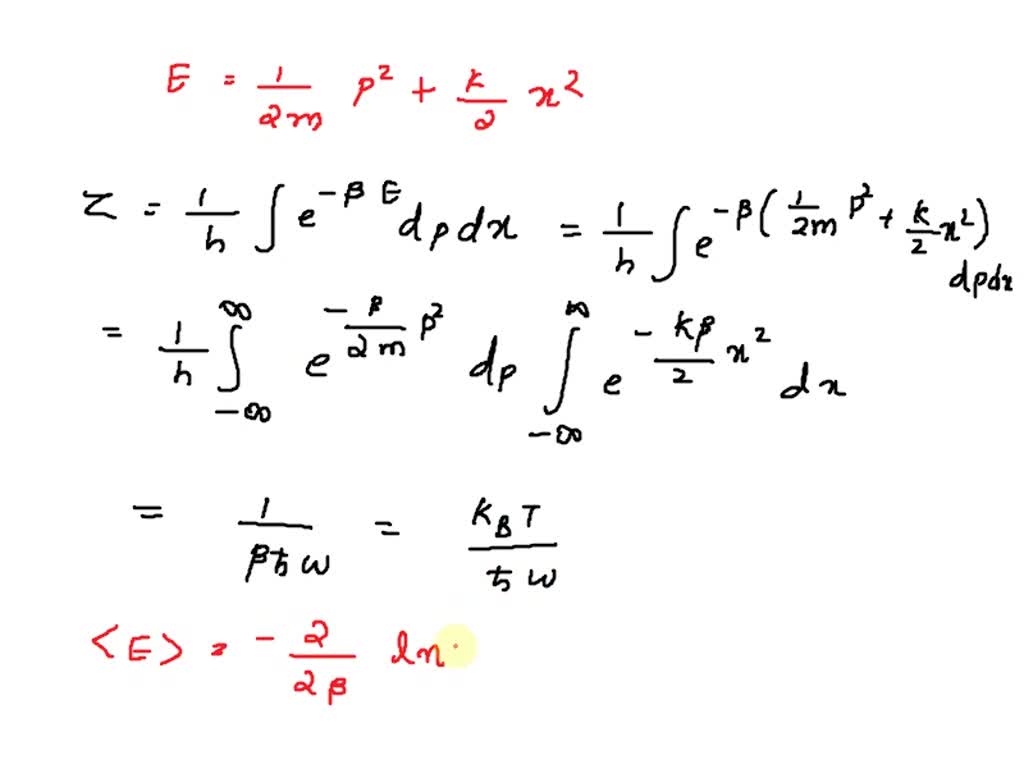
SOLVED: Consider a system of many identical harmonic oscillators. Each harmonic oscillator has its energy of , 2) ho with n-0, 1,2, 8. Assuming they are distinguishable; (a) find the partition function
Statistical physics
Statistical physics
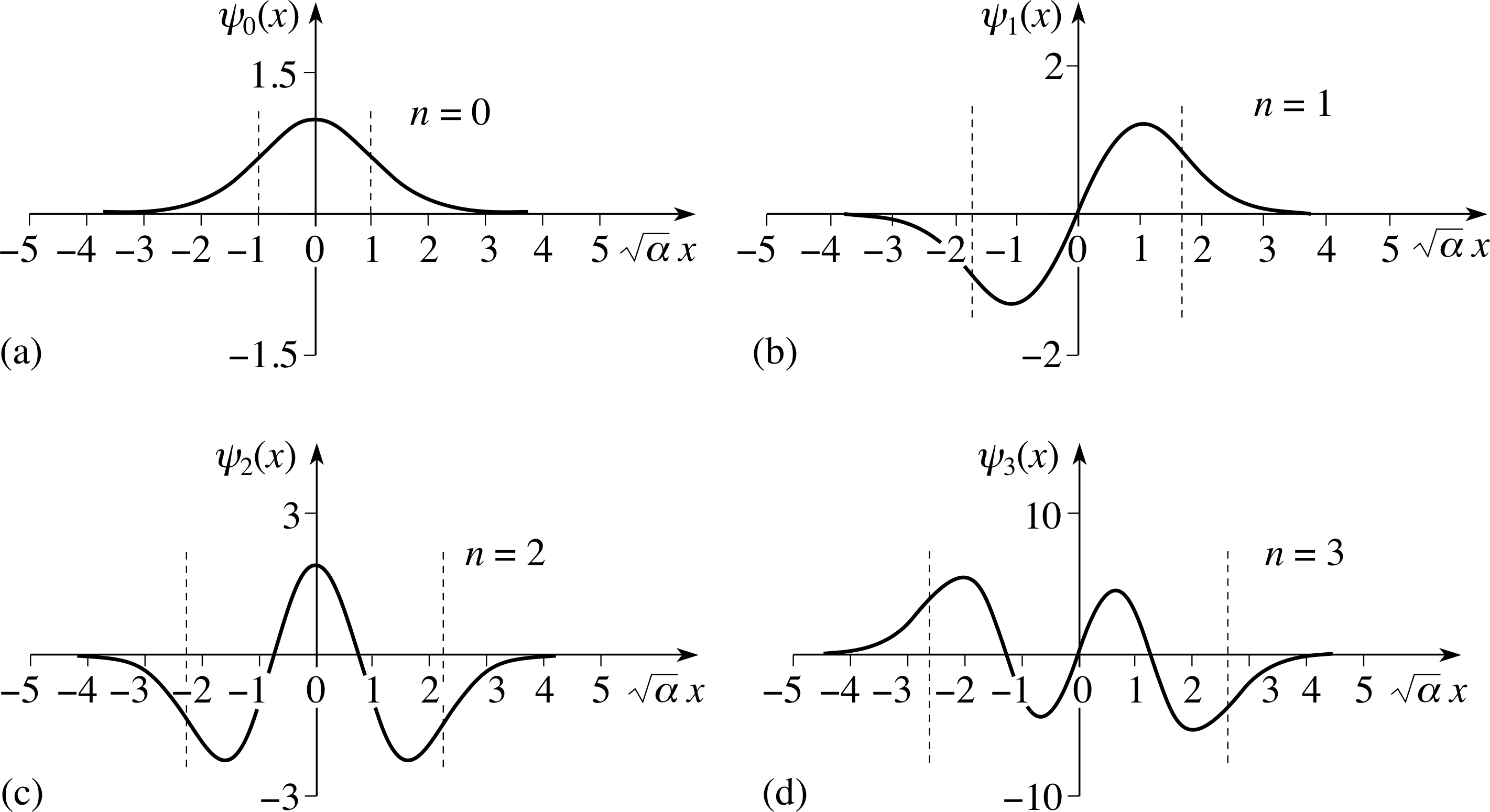
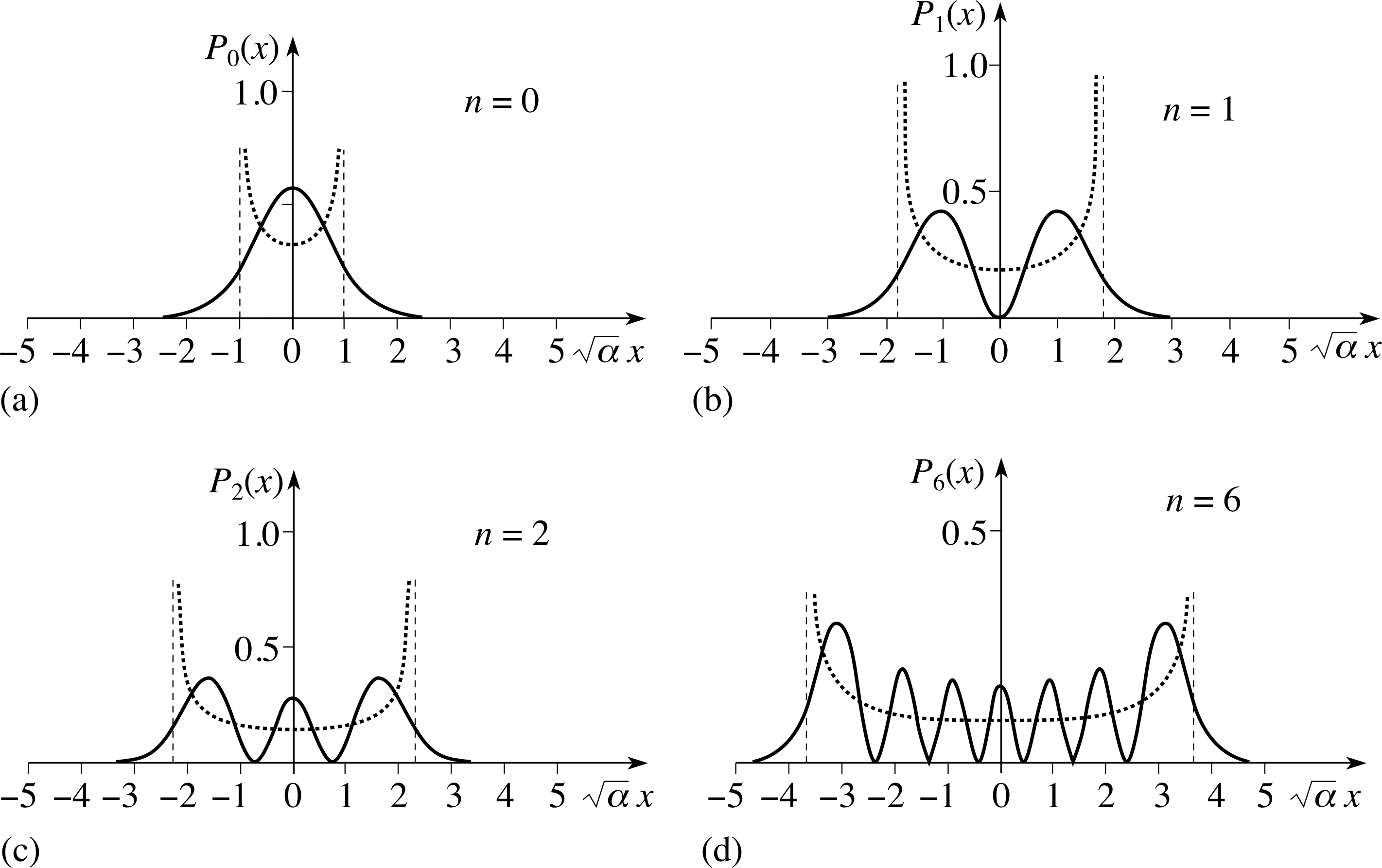
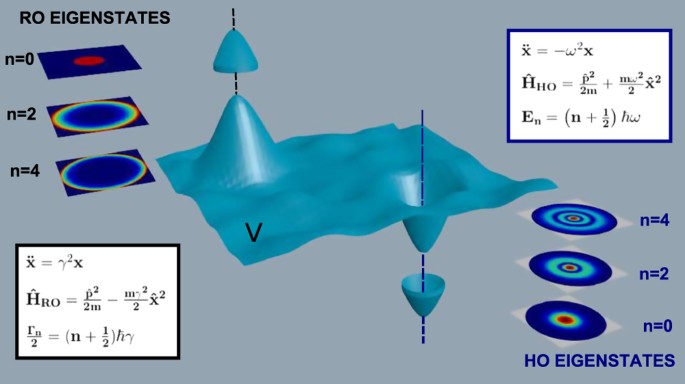
Quantum dynamics of the classical harmonic oscillator: Journal of Mathematical Physics: Vol 62, No 4
Ch3 - QHOs - Statistical Mechancis of Quantum Harmonic Oscillators - Chapter 3 Statistical Mechanics - Studocu
Physical realization of the Glauber quantum oscillator | Scientific Reports
